Enhancing Greyscale Image Contrast through Histogram Equalisation

May 22, 2023
Freddy

Image processing is an integral subfield of computer vision, a field which has been on the rise as part of AI. In this article, we take a look at histogram equalisation: an important tool to increase image contrast. We focus exclusively on greyscale images.

Let’s start with a demo.

The upper image is the original image and the lower image is the enhanced image. You can also upload your own image. (Note: The program assumes your image is greyscale. It will always output a greyscale image.)

(Source code)

Pretty neat, right?

The program above uses a technique called histogram equalisation. The fundamental motivation behind histogram equalisation is to increase contrast of images. Image enhancing has many use cases, such as increasing quality of a retro photograph for forensic analysis (or just to make it look nicer!) and preprocessing medical scans before feeding them to train a convolutional neural network.

Disclaimer: In this article, we only consider greyscale images.

Histogram equalisation is mainly used for greyscale images, but it is also possible to apply this on colour images. We explore this in another article.

Histogram equalisation does not always increase contrast, especially if the original image is already very vibrant. Therefore, this technique is usually applied when the original image has low contrast.

How does histogram equalisation work?

If we want to enhance contrast of an image, we must spread out its pixel intensities. The easiest way to achieve this without considering the surroundings of each pixel would be to define a one-to-one mapping from each pixel intensity to a new one.

For example, here’s the (cropped) mapping for the example hills photo. Note that intensity values range from 0 (black) to 255 (white).

Original intensity	133	134	135	136	137	138	139
New intensity	20	26	35	46	58	64	77

How do we define the mapping?

We start by counting the number of pixels with each intensity, then build a histogram of pixel intensities.

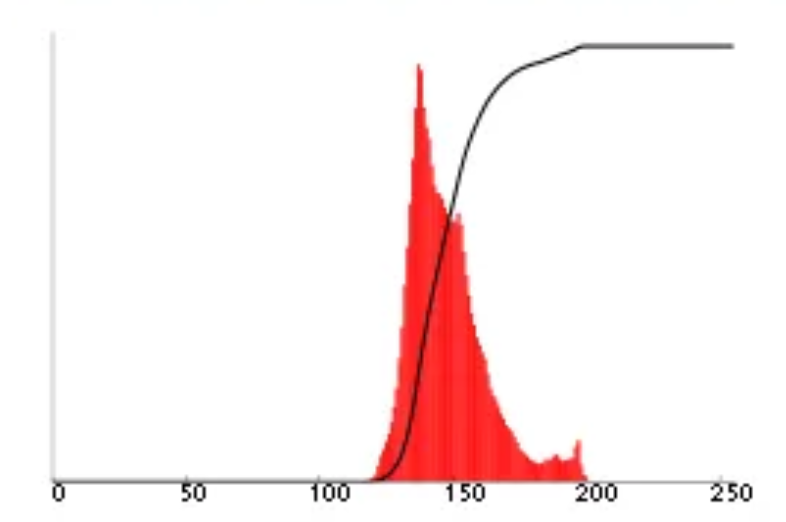
We also plot the CDF (i.e. the black line). The idea is to define the mapping so that the new CDF resembles a straight line.

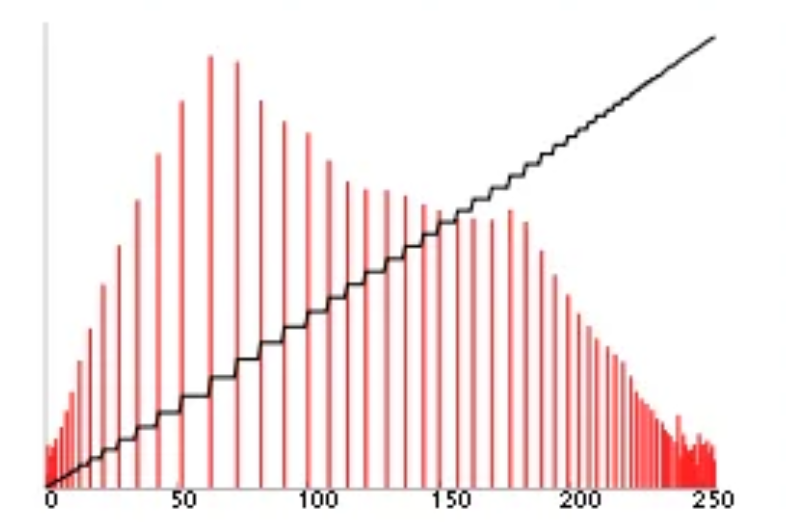
This is how histogram equalisation works visually. Now, let’s formally describe its mathematics!

Behind the scenes: Mathematics

Let $x$ be input image and ${x_{i, j}}$ be intensity of the pixel at ${(i, j)}$.

Define the normalised histogram of $x$ as:

\[h_\phi = \frac{\sum_{x_{i, j} \in x} \mathbf{1} \left( x_{i, j} = \phi \right)}{\text{# pixels in $x$}} \quad \forall \phi \in [0, 255]\]

Note that ${\mathbf{1}}$ denotes the indicator function.

Then equalisation application is defined as:

\[g(x_{i, j}) = \text{floor} \left( 255 \sum_{\phi=0}^{x_{i, j}} h \phi \right)\]

Let’s code histogram equalisation!

Histogram equalisation is so useful that it is included in almost every mainstream programming library, especially Python: pillow, scikit-image, PyTorch etc.

However, for learning purposes, let’s code this in vanilla JavaScript! The function below takes in a list of pixels (input image) and returns a list of pixels (equalised image).

Treat the code below for learning purposes only. It's very efficient in JavaScript - since nothing is parallised! (Also, JavaScript is generally slow as an interpreted language.) For large images, the same implementation in Python using NumPy will run a lot faster.

function equalise(pixels) {
    // Pre: image is greyscale but in RGBA format
    
    // Intensity histogram
    const histogram = Array(256).fill(0);

    // += 4 since image is in RGBA format, so we consider every 4th value only
    for (let i = 0; i < pixels.length; i += 4) {
        index = pixels[i];
        histogram[index]++;
    }

    // Normalise histogram and create pixel mapper from cumulative histogram
    const mapper = [];
    let sum = 0;

    for (let i = 0; i < histogram.length; i++) {
        // Normalise histogram
        histogram[i] /= (pixels.length / 4);

        // Keep track of CDF
        sum += histogram[i];

        // Translate the maths formula to code
        mapper.push(Math.floor(sum * (histogram.length - 1)));
    }

    // Update pixels
    for (let i = 0; i < pixels.length; i += 4) {
        intensity = mapper[pixels[i]];

        pixels[i] = intensity;
        pixels[i + 1] = intensity;
        pixels[i + 2] = intensity;
    }

    return pixels;
}

I used this snippet of code for the interactive demo at the start of this article. In JavaScript, fetching the pixel data from an image is not trivial and involves rendering the image onto a canvas. You can find the source code here.

Enhancing Greyscale Image Contrast through Histogram Equalisation

How does histogram equalisation work?

Behind the scenes: Mathematics

Let’s code histogram equalisation!

Further reading

More Blog Posts